Contents
Ejercicio 1
x = [10 20 40 60 80]'; y = [x log(x)]'; fprintf('Numero\tln(Numero) \n') fprintf('%5d \t %.4f\n', y)
Numero ln(Numero) 10 2.3026 20 2.9957 40 3.6889 60 4.0943 80 4.3820
Ejercicio 2
prompt1='Introduzca su peso en kg: '; prompt2='Introduzca su altura en metros: '; dlg_title='Cálculo del IMC'; peso=str2double(inputdlg(prompt1,dlg_title)) altura=str2double(inputdlg(prompt2,dlg_title)) imc=peso/altura^2; if imc<16 disp(['Su IMC es: ' num2str(imc) '. Infrapeso: delgadez extrema']) elseif imc<16.99 disp(['Su IMC es: ' num2str(imc) '. Infrapeso: delgadez moderada']) elseif imc<18.49 disp(['Su IMC es: ' num2str(imc) '. Infrapeso: delgadez aceptable']) elseif imc<24.99 disp(['Su IMC es: ' num2str(imc) '. Peso normal']) elseif imc<29.99 disp(['Su IMC es: ' num2str(imc) '. Sobrepeso']) elseif imc<34.99 disp(['Su IMC es: ' num2str(imc) '. Obeso: Tipo I']) elseif imc<40 disp(['Su IMC es: ' num2str(imc) '. Obeso: Tipo II']) elseif imc>40 disp(['Su IMC es: ' num2str(imc) '. Obeso: Tipo III']) end
peso =
75
altura =
1.8000
Su IMC es: 23.1481. Peso normal
Ejercicio 3
Cambiamos el número 15 en base decimal a base hexadecimal:
cambia_base(15,16)
f
Funcion usada para este ejercicio:
% function cambia_base(n,b) % basecad = '0123456789abcdef'; % if (n>=b) % cambia_base(idivide(int64(n),int64(b)),b); % end % fprintf(basecad(mod(n,b)+1)) % disp(' ') % end
Ejercicio 4
Hacemos el caso pedido:
syms x for i=[-0.75 -0.5 0 0.5 1.4] Valor_inicial=i sol=double(Ej4fun(x^3-sin(x),i,0.01)) end % Funcion usada para este ejercicio: % function [Xn]=Ej4fun(fun,Xn,tol) % syms x % der = diff(fun,x); % error = 1; % tolerancia = tol; % while error>=tolerancia % X1 = Xn - (subs(fun,Xn)/subs(der,Xn)); % error = abs((X1-Xn)/X1); % Xn=X1; % end % end
Valor_inicial =
-0.7500
sol =
-0.9286
Valor_inicial =
-0.5000
sol =
0.9287
Valor_inicial =
0
sol =
0
Valor_inicial =
0.5000
sol =
-0.9287
Valor_inicial =
1.4000
sol =
0.9286
Ejercicio 5
R1=100;R2=200;R3=50;R4=100;R5=300;Ta=50;Qc=25; A=[R1 0 0 0 -1 1 0;0 R2 0 0 0 -1 1;0 0 R3 0 -1 0 0; 0 0 0 R4 0 -1 0; 0 R5 0 0 0 0 -1; 1 0 1 0 0 0 0; 1 -1 0 -1 0 0 0] b=[0 0 -Ta -Ta -Ta Qc 0]' sol=A\b; fprintf('Q1\t\t Q2\t\t Q3\t\t Q4\t\t Tc\t\t Tp\t\t Tw\t\t \n') fprintf('%5d \t %5d \t %5d \t %5d \t %5d \t %5d \t %.4f\n', sol')
A =
100 0 0 0 -1 1 0
0 200 0 0 0 -1 1
0 0 50 0 -1 0 0
0 0 0 100 0 -1 0
0 300 0 0 0 0 -1
1 0 1 0 0 0 0
1 -1 0 -1 0 0 0
b =
0
0
-50
-50
-50
25
0
Q1 Q2 Q3 Q4 Tc Tp Tw
5.357143e+00 8.928571e-01 1.964286e+01 4.464286e+00 1.032143e+03 4.964286e+02 317.8571
Ejercicio 6
R1=100;R2=200;R3=50;R4=100;R5=300;Ta=50;Qc=25; A=[R1 0 0 0 -1 1 0;0 R2 0 0 0 -1 1;0 0 R3 0 -1 0 0; 0 0 0 R4 0 -1 0; 0 R5 0 0 0 0 -1; 1 0 1 0 0 0 0; 1 -1 0 -1 0 0 0]; b=[0 0 -Ta -Ta -Ta Qc 0]'; fprintf('La matriz solución es:\n') sol=A\b fprintf('Con la matriz solución hacemos la condición:\n\n') disp(['La condición de la matriz es ' num2str(cond(sol))]) fprintf('\nTambién hacemos la norma 1:\n') norma_1=norm(sol,1) fprintf('La norma 2:\n') norma_2=norm(sol,2) fprintf('La norma inf:\n') norma_inf=norm(sol,inf) fprintf('La norma Frobenius:\n') norma_fro=norm(sol,'fro') fprintf('Posteriormente hacemos la factorización LU:\n\n') [L,U]=lu(A) fprintf('Por último, hacemos la comprobación:\n') sol_lu=inv(U)*inv(L)*b
La matriz solución es:
sol =
1.0e+03 *
0.0054
0.0009
0.0196
0.0045
1.0321
0.4964
0.3179
Con la matriz solución hacemos la condición:
La condición de la matriz es 1
También hacemos la norma 1:
norma_1 =
1.8768e+03
La norma 2:
norma_2 =
1.1888e+03
La norma inf:
norma_inf =
1.0321e+03
La norma Frobenius:
norma_fro =
1.1888e+03
Posteriormente hacemos la factorización LU:
L =
1.0000 0 0 0 0 0 0
0 0.6667 0 0 0 1.0000 0
0 0 1.0000 0 0 0 0
0 0 0 1.0000 0 0 0
0 1.0000 0 0 0 0 0
0.0100 0 0.0200 0 1.0000 0 0
0.0100 -0.0033 0 -0.0100 0.3333 0.0167 1.0000
U =
100.0000 0 0 0 -1.0000 1.0000 0
0 300.0000 0 0 0 0 -1.0000
0 0 50.0000 0 -1.0000 0 0
0 0 0 100.0000 0 -1.0000 0
0 0 0 0 0.0300 -0.0100 0
0 0 0 0 0 -1.0000 1.6667
0 0 0 0 0 0 -0.0311
Por último, hacemos la comprobación:
sol_lu =
1.0e+03 *
0.0054
0.0009
0.0196
0.0045
1.0321
0.4964
0.3179
Ejercicio 7
fprintf('Hallamos los autovalores y autovectores de la siguiente matriz:\n') A=[0 1 -1;-6 -11 6;-6 -11 5] [vectores valores] = eig(A) fprintf('Ante las dos matrices anteriores, la primera de ellas contiene\nlos vectores propios en forma de columna, mientras que la segunda matriz "valores"\nalmacena en la diagonal principal los valores propios correspondientes a cada columna de la matriz "vectores"')
Hallamos los autovalores y autovectores de la siguiente matriz:
A =
0 1 -1
-6 -11 6
-6 -11 5
vectores =
0.7071 -0.2182 -0.0921
0.0000 -0.4364 -0.5523
0.7071 -0.8729 -0.8285
valores =
-1.0000 0 0
0 -2.0000 0
0 0 -3.0000
Ante las dos matrices anteriores, la primera de ellas contiene
los vectores propios en forma de columna, mientras que la segunda matriz "valores"
almacena en la diagonal principal los valores propios correspondientes a cada columna de la matriz "vectores"Ejercicio 8
fprintf('Las tensiones V1 y V2 son: \n\n') A=[1.5-2*i -.35+1.2*i;-.35+1.2*i 0.9-1.6*i]; b=[20+40*i; 20+15*i]; sol=A\b; fprintf('V1\t\t V2 \n') fprintf('%5d \t %.4f\n', sol) fprintf('\n La potencia generada por la fuente de la izquierda es de: \n') S_izq=sol(1)*30+40*i fprintf('La potencia generada por al fuente de la derecha es de: \n') S_der=sol(2)*20+15*i
Las tensiones V1 y V2 son: V1 V2 5.813011e+03 5739.0335 La potencia generada por la fuente de la izquierda es de: S_izq = 1.7445e+05 La potencia generada por al fuente de la derecha es de: S_der = 1.1480e+05
Ejercicio 9
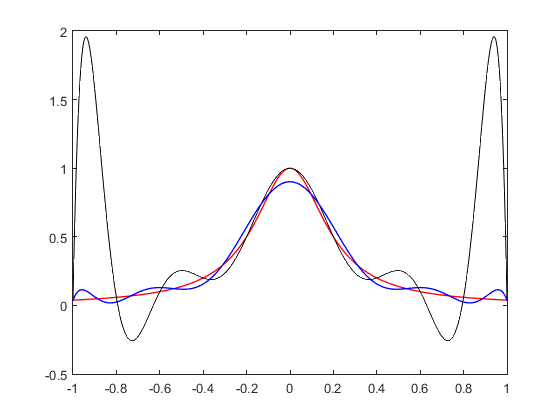
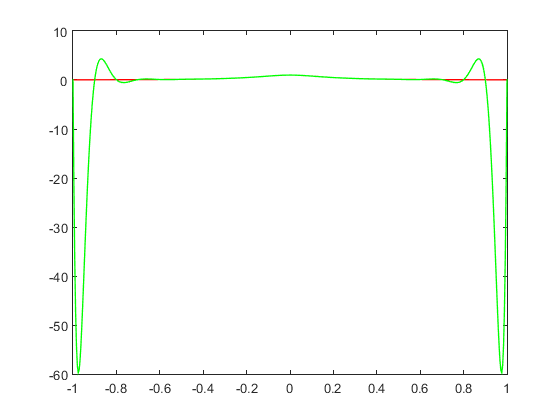
f=@(x) 1./(1+25*x.^2); x=linspace(-1,1,500); y_true=f(x); figure; plot(x,y_true,'r','linewidth',1); hold on; N=10; xint=linspace(-1,1,N+1); yint=zeros(1,n1); y=f(xint); n1=length(x); for i=1:n1 yint(i)=Lagrange(xint,y,x(i)); end plot(x,yint,'k') hold on p=polyfit(xdata,ydata,N); y_fit=polyval(p,x); poly_10=plot(x,y_fit,'b','linewidth',1); hold on; figure plot(x,y_true,'r','linewidth',1); hold on N=20; xdata=linspace(-1,1,N+1)'; ydata=f(xdata); p=polyfit(xdata,ydata,N); y_fit=polyval(p,x); poly_20=plot(x,y_fit,'g','linewidth',1); hold on; fprintf('\nEn la figura 1 se representan:\nEn rojo la función original.\nEn negro la función aproximada usando Lagrange (10 puntos).\nEn azul, la función aproximada usando polyfit (10 puntos).\n\nEn la figura 2 se observa en rojo la función original y en verde \nla función aproximada usando polyfit con 20 puntos.\n\n ') % Función de Lagrange usada: % function Yint=Lagrange(x,y,Xint) % n=length(x); % L=ones(1,n); % Yint=0; % for i=1:n % L(i)=1; % for j=1:n % if j~=i % L(i)=L(i)*(Xint-x(j))/(x(i)-x(j)); % end % end % end % Yint=sum(y.*L); % end
En la figura 1 se representan: En rojo la función original. En negro la función aproximada usando Lagrange (10 puntos). En azul, la función aproximada usando polyfit (10 puntos). En la figura 2 se observa en rojo la función original y en verde la función aproximada usando polyfit con 20 puntos.
Ejercicio 10
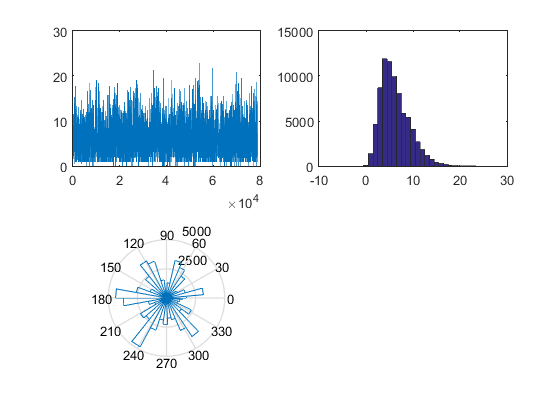
lista=xlsread('winddata.xlsx'); %Apartado a) subplot(2,2,1) plot(lista(:,4)) %Apartado b) subplot(2,2,2) n=0:25; hist(lista(:,4),n); %Apartado c) subplot(2,2,3) n=linspace(0,2*pi,36); rose(lista(:,4),n); hold off
Ejercicio 11
x1=-4:0.3:4; y1=-4:0.3:4; [x,y]=meshgrid(x1,y1); figure surf(x,y,sin(x).*cos(y).*exp(-(x.^2+y.^2).^0.5))
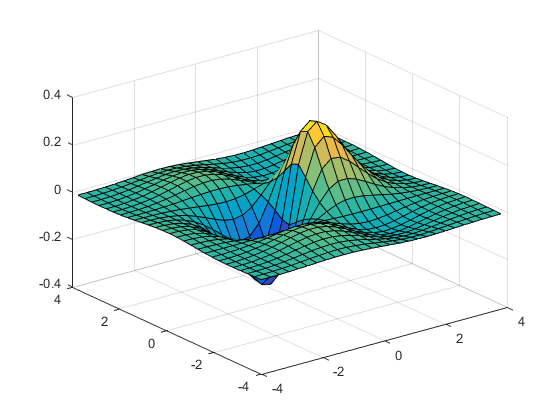
Ejercicio 12
Siguiendo las directrices propuestas en el enunciado, tal y como se propone:
figure Ejemploode

Las funciones usadas en este ejercicio han sido
% function Ejemploode % [t, yy] = ode45(@HalfSine, [0 35], [1 0], [ ], 0.15); % plot(t, yy(:,1)) % function y = HalfSine(t, y, z) % h = sin(pi*t/5).*(t<=5); % y = [y(2); -2*z*y(2)-y(1)+h];
Ejercicio 13
Tal y como se muestra en el ejemplo de los apuntes, aquí están representadas otras funciones:
k = 5; m = 10; fo = 10; Bo = 2.5; N = 2^m; T = 2^k/fo; ts = (0:N-1)*T/N; df = (0:N/2-1)/T; SampledSignal = Bo*sin(2*pi*fo*ts) + Bo/2*sin(2*pi*fo*2*ts); An = abs(fft(SampledSignal, N))/N; subplot(2,2,1) plot(df, 2*An(1:N/2)) SampledSignal1 = exp(-2*ts).*sin(2*pi*fo*ts); An1 = abs(fft(SampledSignal1, N))/N; subplot(2,2,2) plot(df, 2*An1(1:N/2)) SampledSignal2 = sin(2*pi*fo*ts + 5*sin(2*pi*fo/10*ts)); An2 = abs(fft(SampledSignal2, N))/N; subplot(2,2,3) plot(df, 2*An2(1:N/2)) SampledSignal3 = sin(2*pi*fo*ts - 5*exp(-2*ts)); An3 = abs(fft(SampledSignal3, N))/N; subplot(2,2,4) plot(df, 2*An3(1:N/2))
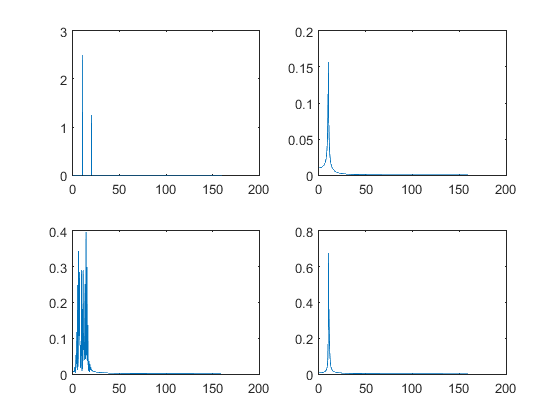
Ejercicio 14
%Simplemente ejecutar
figure
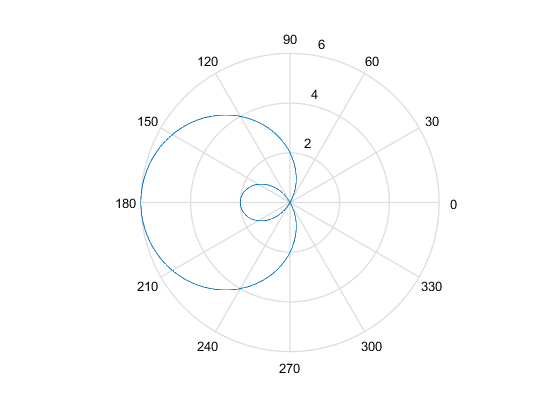
theta = linspace(-pi, pi, 300);
p = 2-4*cos(theta);
polar(theta, p)